Raul Ibáñez ha dedicado su última sección de matemáticas al recuerdo de la figura de un gran divulgador de las matemáticas.

El pasado 21 de octubre se cumplieron 100 años del nacimiento del divulgador de las matemáticas Martín Gardner. Desde su muerte en 2010, todos los años se celebra el evento Martin Gardner Global Celebration of Mind Gathering de forma simultánea en multitud de lugares del mundo, alrededor de la fecha de su nacimiento.

Martin Gardner (Oklahoma, EEUU, 1914-2010). No era matemático, sino filósofo (aunque su elección inicial había sido la física), pero se dedicó a trabajar de escritor y periodista para ganarse la vida.

Su interés por la ciencia, la magia y las recreaciones científicas le llevarían a iniciar el viaje más apasionante de su vida en 1957, la sección “Juegos Matemáticos” de la revista American Scientific que escribiría durante 25 años, y que le acabaría convirtiendo en el mayor divulgador de las matemáticas de todos los tiempos, y en un experto en matemática recreativa.

Durante ese viaje desarrollaría una investigación personal sobre las recreaciones matemáticas, y más tarde sobre infinidad de temas matemáticos, para poder explicarlos en sus libros y artículos. Contactaría con la colaboración de grandes matemáticos, que lo respetaban por la profundidad de sus ideas. Pero lo que le convertiría en el mayor divulgador de las matemáticas fue su estilo, la manera que tenía de presentar los temas (el estilo Gardner), la sencillez de la explicación e incluso del lenguaje utilizado, pero manteniendo el interés e importancia del tema tratado, lo que cautivaría al público general, pero también a matemáticos y científicos. En su humildad decía que “Me llevaba tanto tiempo entender aquello sobre lo que escribía que aprendía cómo escribirlo para que la mayoría de los lectores lo entendieran”. Es de destacar además su faceta como uno de los abanderados del movimiento de “escepticismo científico”…

Pero si hablamos de Martin Gardner, debemos de hablar de juegos y problemas de ingenio, que eran su especialidad.

1. Juegos de ingenio con chocolate. Aprovechando que la semana pasada escribí una entrada en el Cuaderno de Cultura Científica titulada “Juegos matemáticos con chocolate” vamos a ver alguno de esos juegos…

El primero de los juegos que vamos a analizar aquí, suele recibir el nombre “partiendo tabletas de chocolate” (“breaking chocolate bars”) y consiste en lo siguiente. Es un juego para dos personas que, por turnos, se dedican a partir una tableta de chocolate, por ejemplo, de tamaño 6 x 4. Pero, solo se puede partir la tableta de chocolate por las líneas horizontales y verticales, como de hecho, se hace en la realidad. Es decir, el corte es de toda la línea, de un lado a otro.

Por ejemplo, en la primera ronda, el primer jugador podría partir por la línea vertical intermedia, generando dos piezas de tamaño 3 x 4, y el segundo jugador tomar una de las piezas 3 x 4, y partirla por la primera línea horizontal, empezando por abajo, generando así una pieza 3 x 1 y otra 3 x 3. En ese punto de la partida, habrá tres trozos de chocolate, de tamaños 3 x 4, 3 x 1 y 3 x 3.

Los jugadores seguirán cortando hasta que solamente queden onzas sueltas, es decir, piezas 1 x 1, y no se pueda partir más. La persona que hace la última división gana, o lo que es lo mismo, pierde el jugador que se queda sin la posibilidad de fragmentar más el chocolate.

Como en este juego no se puede quedar en tablas, empate, necesariamente gana uno de los dos jugadores. Os dejo la siguiente cuestión… ¿existe alguna forma de ganar siempre a este juego? ¿Quién gana, el jugador que juega el primero, o el segundo? La solución es pensar cuantos cortes se pueden realizar hasta que todas las onzas queden sueltas.

El siguiente juego, que recibe el nombre de “yucky choccy” (que podríamos traducir como “chocolate asqueroso”), lo descubrí en el excelente libro “Locos por las matemáticas” de Ian Stewart. De nuevo, este juego se juega con una tableta de chocolate rectangular, o cuadrada, típica, pero con la particularidad de que la onza de una de las esquinas (en nuestra imagen siguiente es la de arriba a la izquierda) tiene mal sabor, está asquerosa (ya sea porque le ha caído un poco de jabón, como dice Stewart, o porque tiene una almendra podrida).

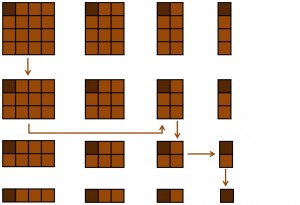Los jugadores, por turnos, partirán el chocolate por una línea horizontal o vertical (de nuevo, debe de ser toda la línea), con la intención de comerse uno de los trozos de chocolate que parten, en concreto el que no incluya la onza asquerosa. Al final, el jugador que se come la onza asquerosa pierde.

Este es un juego interesante, al que podéis jugar, y del que podéis analizar cual es la estrategia ganadora, y para qué jugador.

2. El puzzle de los tetraminós. Uno de los temas que popularizó Gardner, y del que ya hemos hablado aquí en alguna ocasión fueron los Pentominós, asociados a los cuales existen una gran cantidad de juegos, incluso comerciales, como el Katamino, el Blokus, o Top This. A partir de los pentominós, el informático ruso xx inventó el Tetris, que utiliza los tetraminós. Y es con las piezas del Tetris con las que vamos a plantear un puzzle…

Los tetraminós son piezas geométricas planas formadas conectando cuatro cuadrados por alguno de sus lados. Los cuadrados se conectan lado con lado, pero no se pueden conectar ni por sus vértices, ni juntando solo parte de un lado de un cuadrado con parte de un lado de otro.

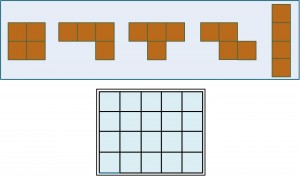Existen cinco tipos de tetraminós distintos (que se denotan por la similitud con la forma de alguna de las letras del abecedario, como I, L, O, T, Z). Las piezas L y Z podrían tener sus simétricos si no abandonamos el plano, pero olvidémonos de ellas.

El puzzle de los tetraminós: formar un rectángulo de tamaño 5 x 4 con los cinco tetraminós distintos (I, L, O, T, Z).

Lo dejo como problema para quienes estáis escuchando este programa. Os recuerdo que la solución a este puzzle puede ser positiva, es decir, es posible formar un rectángulo 5 x 4, y esto se demuestra construyéndolo directamente, o podría ser negativa, y habría que demostrar que no es posible realizar el puzzle, lo cual es más complejo.

Con motivo del centenario del nacimiento de Martin Gardner han salido, o van a salir, dos publicaciones especiales…

A. Investigación y Ciencia, en su colección TEMAS, ha sacado un número (el 77) dedicado a este divulgador… con el título… EL UNIVERSO MATEMÁGICO DE MARTIN GARDNER, Juegos, acertijos, paradojas y otras maravillas recreativas. Aparecen por ejemplo “Flexágonos”, que fue su primer artículo en Scientific American, “El juego de la vida” (el famoso juego de John H. Conway), “De números y juegos” (juegos de estrategia de John H. Conway), “Los embaldosados de Penrose” (mosaicos no periódicos), “Ocho rompecabezas y un juego”, y muchos más…

B. VVAA, Gardner para principiantes, Biblioteca de Estímulos Matemáticos, SM-RSME, 2014.

Entre los artículos que aparecen están… “Las sin cuenta caras de un papel” (Pedro Alegría), “Paradojas” (M. A. Morales -Gaussianos), “Matemáticas para divertirse: juegos de estrategia” (Maria Luz Callejo), “El juego de la rana y otros juegos de intercambio” (R. I.), “Códigos secretos” (Ana de la Fuente), “Juegos de adivinación y matemáticas” (Vicente Meavilla), “Magia con ocho cartas” (Jorge Luengo, Isabel Queralt), etc…

C. Y además, la editorial Páginas (de temas de magia) está preparando la traducción de la autobiografía de Martin Gardner en castellano, que se publicará en breve también…