Los miércoles, a partir de las 23:30 de la noche, se emite en La 2 Orbita Laika, un un latenight de ciencia en el que participa, entre otros mucho ilustres divulgadores, el matemático Raul Ibáñez. En tiempo record Raul explica en la sección “Una de mates” diferentes conceptos matemáticos como el que hoy nos ocupa: ni más ni menos que un ejercicio de adivinación de números. Raul podría forrarse en Las Vegas con este truco pero como no le van las lentejuelas ha querido compartirlo, y aquí sin tanto límite de tiempo, con los oyentes de La mecánica dle caracol. Esto es lo que nos cuenta:

El truco de Raul

“Para realizar este truco se necesita una calculadora (si estamos en casa, una calculadora normal y corriente, pero si fuese una actuación, debería ser una calculadora gigante) y una persona del público con la que interactuar. Le pedimos a esa persona que multiplique con la calculadora, y sin que “el mago” (yo en este caso) lo vea, diez o doce números de una cifra, los que quiera, por ejemplo, puedes empezar así… el 3 por el 7 por el 5 … eso sí, le advertimos que no multiplique por el 0 –ya que quedaría 0- o por el 1 -que deja la multiplicación igual-, pero por lo demás, que procure elegir un poco al azar, por todo el teclado numérico, para que sea diferentes números…

[supongamos que la multiplicación que realiza es:
5 x 6 x 3 x 4 x 2 x 9 x 7 x 3 x 9 x 8 x 7 x 6 = 411.505.920]

Una vez que ha realizado la multiplicación (sin que el mago la vea, insisto), podemos incluso aventurarnos a decir que el número que le ha salido termina en 0.

Ahora, le pedimos que elija una de las cifras del número que le ha salido tras la multiplicación, que no sea un 0 [imaginemos que del número anterior, 411.505.920, ha elegido el 5]… y una vez que ha hecho su elección le pedimos (quien haga de mago claro) que nos diga el resto de las cifras del número en el orden que le apetezca… y nosotros (el mago) intentaremos adivinar cuál es el número que ha elegido…

[En nuestro ejemplo, la persona podría ir diciendo los demás números, una vez seleccionado un 5, que serían… 0… 2… 9… 0… 5… 1… 1… y 4…] … y entonces, adivinaríamos el número, en nuestro ejemplo que el número que ha elegido es el 5.

Expliquemos ahora las matemáticas que nos permiten hacer este truco… utilizamos la regla de divisibilidad del 9… que nos dice que un número es divisible por 9 si al sumar las cifras que lo componen el resultado también es divisible por 9, por ejemplo, el número 3.492 es divisible por 9, ya que 3 + 4 + 9 + 2 = 18, que es divisible por 9.

El número que ha obtenido la persona después de varias multiplicaciones también es divisible por 9, puesto que en la multiplicación habrá utilizado seguramente el 3, el 6 y el 9, y al multiplicarlos el resultado es claramente divisible por 9.

Entonces lo que yo he hecho es lo siguiente… he sumado los números que me ha ido diciendo… así 0 + 2 + 9 + 0 + 5 + 1 + 1 + 4 = 22, y el siguiente número divisible por 9 es el 27, y nos falta un 5 para llegar a él, 22 + 5 = 27, por lo tanto, el número que ha elegido, y no me ha dicho, es el 5…

Respecto, a que habíamos adivinado que el número terminaba en 0, se debe a que seguramente en la multiplicación se habrá multiplicado probablemente por 5 y un par, de ahí, 2 x 5 =10, el cero.

Y ahora vosotros podéis ser los magos… además, podéis ver el video de Órbita Laika del truco en el Cuaderno de Cultura Científica.

Un truco parecido al anterior, pero que podemos hacer sin la ayuda de una calculadora, es el siguiente. Le pedimos a una persona que piense un número de 4 cifras y que no nos lo diga [por ejemplo, imaginemos que ha pensado el 7.259], entonces que sume las cifras del número [en este caso, 7 + 2 + 5 + 9 = 23], y finalmente que reste este resultado a su número original [en nuestro caso, 7.259 – 23 = 7.236].

Ahora, vamos a decirle que piense en una de las cifras del número que ha obtenido, que se la guarde para ella y que nos diga el resto de las cifras, en el orden que quiera, entonces adivinaremos cual es el número que ha pensado. El truco es de nuevo la regla de divisibilidad del 9, ya que si a un número de 4 cifras le restamos la suma de sus cifras, entonces siempre es divisible por 9.

[en nuestro caso, si eligió, por ejemplo, el 3 (del 7.236), nos dirá el resto de números, que iremos sumando, 6 + 2 + 7 = 15 y el siguiente múltiplo de 9 es el 18, y le faltan 3 al 15 para sumar 18, luego 3 es el número elegido]

Expliquemos el motivo de que la resta de un número de 4 cifras de la suma de sus cifras sea múltiplo de 9. Si el número es el abcd, eso quiere decir que es el número (1000 x a + 100 x b + 10 x c + d), y si le restamos (a+b+c+d), nos dará 999 x a + 99 x b + 9 x c = 9 x (111 x a + 11 x b + c), luego múltiplo de 9. Más aún, vale para cualquier número con cualquier cantidad de cifras.

Ahora otro truco más de adivinación. Para empezar el mago matemático explica que va a realizar una predicción, escribe un número en un papel y lo deja aparte (en un sobre cerrado o se lo da a una persona del público, pero sin que pueda verlo).

Elige a una persona del público, que le va a ayudar, y le pide:

i) que piense en un número de tres cifras [por ejemplo, 537];
ii) que cambie el primer dígito y el último, que deben claro ser distintos [así en nuestro caso, 735];
iii) reste el menor al mayor [para nosotros, 735 – 537 = 198];
iv) ahora cambia el primer dígito y el último de este número, y suma ambos números [198 + 891 = 1089]… 1089!!

(nota: todas esas operaciones las puede hacer en alto, para que las escuche todo el mundo, ya que la predicción del mago no se va a tocar… aunque se podría hacer sin que la persona lo diga, solo el resultado)

v) le pides a alguien que mire el sobre con la predicción, y resulta que es el número… 1089.

Esta es una de las propiedades matemáticas del número 1089. Si se coge un número cualquiera de tres cifras, se cambia la primera y la última, se restan ambos, y al número obtenido se le suma el número que se obtiene al cambiarle a ese la posición de la primera y la última cifra, se obtiene siempre 1089, como se puede demostrar fácilmente.

Algo similar ocurre si en lugar de un número de tres cifras se realiza el truco con un número con más cifras. Por ejemplo, si se hace con un número de 5 cifras, el número final será 109989, es decir, por cada cifra a partir de 3 se va añadiendo un nueve en el centro de 1089.

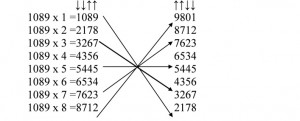
El número 1089 es un número mágico. Por ejemplo, si le multiplicamos por 9 se obtiene el simétrico… 1089 x 9 = 9801. E igual con los otros mencionados… 109989 x 9 = 989901.

Otro número, además del 1.089, cuyo reverso es múltiplo de sí mismo, es el número 2.718, ya que al multiplicarlo por 4 se obtiene su reverso, 2.718 x 4 = 8.172.

Más aún, respecto al 1089…

Para terminar podríamos hacer el siguiente juego a nuestros, y nuestras, oyentes. Cada uno de ellos deben de considerar un número de tres cifras [por ejemplo, el 537]. Ahora lo que tienen que hacer es poner ese mismo número dos veces, una seguida de la otra, creando un número de 6 cifras [en nuestro ejemplo, 537.537]. Cada oyente en su casa debe dividirlo por 7, entonces a aquellos oyentes que les de 6 de resto en la división, se les enviarán 60 euros, a los que les de 5 serán 50 euros, así hasta 10 euros para los que tengan un 1 de resto, y nada para quienes la división sea exacta, es decir, de resto 0.

Para el número que hemos elegido nosotros, el 537, tenemos 537.537 : 7 = 76.791 (y de resto 0)… mala suerte yo no gano ningún euro, ¿y nuestros oyentes?

Pues la verdad es que tampoco ganan nada, ya que la división tiene siempre resto 0. ¿Por qué? Al repetir nuestro número lo que ocurre es que estamos multiplicando nuestro número por 1.001 (i.e. 537.537=1.001 x 537), pero 1.001 = 7 x 143, luego el número que hemos creado 537.537 es divisible por 7, y el resto siempre es 0!.

Y tras compartir con nosotros el secreto de la adivinación de los números Raul nos deja un problema a resolver en las dos próximas semanas.

Doce monedas de oro

Un anticuario posee un grupo de doce monedas de oro, y sabe que una de ellas es falsa. La moneda falsa es menos pesada que las demás, pero el anticuario solo dispone de una balanza antigua, de dos platos y sin pesos. ¿Es posible que el anticuario descubra cual es la moneda de oro falsa, realizando solo tres pesadas?

La respuesta de Raul ( hay otras más posibles):

La idea consiste en hacer tres grupos de cuatro monedas. En la primera pesada se ponen cuatro monedas en cada plato, y se dejan otras cuatro fuera, lo cual nos permite conocer en cuál de los grupos de cuatro monedas esta la falsa. Y ahora teniendo cuatro monedas, que incluyen a la falsa, se puede conocer cual es la falsa con tan solo dos pesadas, primero dos monedas en cada plato, y una pesada más para distinguir entre las dos que resulten menos pesadas