Recordemos que un cuadrado mágico de orden 3 es una distribución de los primeros 9 números, 1, 2, 3, 4, 5, 6, 7, 8, 9, sobre las casillas de un cuadrado 3 x 3, de forma que la suma de cada fila, cada columna y cada diagonal sea siempre la misma, como en el cuadrado.
Si admitimos la posibilidad de que esté formado por otros números distintos, ¿cuáles son los números que faltan en el siguiente cuadrado mágico?
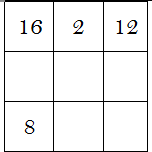
Solución: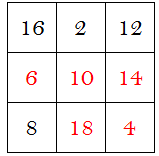


Honatx erantzuna:
16, 2, 12
6, 10, 14
8, 18, 4
Agur bero bat.
16 2 12
6 10 14
8 18 4
Es fácil,
16 2 12
6 10 14
8 18 4
Hace tiempo que no participaba porque he perdido la esperanza de recibir el libro…
Un saludo,
Solución:
16 2 12
6 10 14
8 18 4
Un saludo,
En el caso de los numeros del 1 al 9, la suma de todos ellos es de 45. Por lo tanto cada linea o columna tiene que sumar 15. En este caso, la linea completada, suma 30, por lo que la suma total del cubo tiene que ser de 90.
Contando con que la fila superior esta completa, y la columna izquierda te obliga a que el numero faltante sea un 6, tenemos que buscar 4 numeros que entre ellos sumen 46, pero que ademas, una pareja de ellos, sea superior a la otra en 2, puesto que esta es la diferencia entre las dos filas que faltan por completar.
El resultado en orden de izquierda a derecha, y de arriba abajo es el siguiente:
16,2,12 / 6,19,5 / 8,9,13
16 2 12
6 19 5
8 9 13
Un saludo
Haritz
Problema de cuadrados mágicos.
Kaixo, mi solución es : 2 ,4 ,6 ,8 ,10 , 12 , 14 , 16 , 18.
He llegado del siguiente modo: la suma de la fila es 16 + 2 + 12 = 30 x 3=90, con lo que la suma de todos los números tiene que ser 90 . Sabiendo que en la columna el número que falta es el 6 ,deduzco una serie de números pares que sumen 90 , en la que el centro es el 10.
Hola,
Este es un problema de 4º de EGB en el que nos hinchábamos a hacer cuadrados mágicos.
Una vez que te dabas cuenta de que, conociendo el cuadrado inicial o primero, todos los demás eran el mismo aunque cambiara la proporcionalidad de los términos (la suma cambiaba en la misma proporción) o que la diferencia entre los términos también podía ser diferente de 1, todos los cuadrados se sacan por semejanza (incluye también las rotaciones del cuadrado o las permutaciones de la primera fila por la última o la primera columna por la última).
Si el cuadrado primero es:
4 9 2
3 5 7
8 1 6
El que es el resultado de este problema se ve por semejanza que los términos de la primera fila son los de la última fila del cuadrado primero multiplicado por 2. Aunque en este ejemplo, hay tantos números que sabiendo que la suma de la primera fila es 30, por diferencias se obtienen todos los resultados de los cuadrados.
El resultado sería:
16 2 12
6 10 14
8 18 4
Un saludo,
El cuadrado quedaría así
16. 2. 12
6. 10. 14
8. 18. 4
6+2+12=30
16+8=24 -30=6
12+8=20 -30=10
6+10=16 -30=14
2+10=12 -30=18
12+14=26 -30=4