TeorÃa de grafos
La teorÃa de grafos es una teorÃa que sorprende por su sencillez inicial por su versatilidad, asà como por su fuerza para resolver problemas de lo más variado. Es precisamente su sencillez lo que hace que puedan utilizarse para crear modelos en temas tan dispares, como las telecomunicaciones, Internet, la teorÃa de la información, la quÃmica, la fÃsica, el estudio de probabilidades, en temas de planificación, en el estudio de las redes sociales, en juegos recreativos, en redes neuronales, en programación,â¦
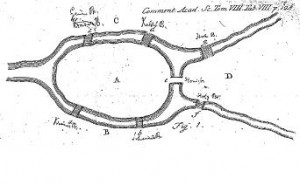
Se suele decir que la teorÃa de grafos se inició con la resolución de Euler del problema de los puentes de Königsberg. Según cuenta la historia, en la ciudad de Königsberg (actualmente Kaliningrado) hacia 1700, sus habitantes se divertÃan con un curioso juego que consistÃa en pasar una vez, y sólo una vez, por cada uno de los siete puentes que cruzaban su rÃo, volviendo al punto de partida.
Para entender este problema es importante saber cómo estaban distribuidos los puentes en el rÃo. Tenemos el rÃo, con sus dos orillas, una isla en medio que está unida a cada una de las orillas por dos puentes hacia cada orilla, después de la isla el rÃo se separa en dos partes, y hay un puente en cada rama del rÃo, y otro puente entre la isla y el terreno entre los dos brazos del rÃo (en total siete puentes).
Podéis intentar resolver vosotros mismos el problema de los puentes de Königsberg, y después de un tiempo, os pasará como a los habitantes de esta ciudad, que no fueron capaces de encontrar el recorrido que resolviera el problema. Entonces, se nos plantean dos cuestiones: a) ¿tiene solución el problema de los puentes de Königsberg? b) Y si no la tiene ¿cómo demostrarlo?
En matemáticas lo que se suele hacer es simplificar los problemas que se están estudiando, eliminando lo que no es importante, para poder crear después un âmodeloâ que describa nuestro problema y sobre el que podamos trabajar matemáticamente para resolverlo. En el problema de los puentes de Königsberg se puede intentar simplificar el problema, como de hecho lo hizo el gran matemático suizo Leonhard Euler (1707-1783).
TeorÃa de grafos
Para ello transformó los elementos que aparecÃan en el problema (puentes, rÃo y zonas de tierra) en un grafo de puntos y aristas que recogiera lo importante del problema, eliminando lo superfluo, para ello cada zona de tierra aislada serÃa un punto, un vértice del grafo, y los puentes son las aristas que unen esos puntos, obteniéndose asà el grafo del problema (nuestro modelo matemático).
Además, hemos planteado un nuevo problema (Las canicas): Tengo una bolsa con canicas. Si las agrupo de 3 en 3, me sobran 2; si las agrupo de 5 en 5, me sobran 3; y si las agrupo de 7 en 7 me sobran 2. Sabiendo que tengo menos de 75 canicas, ¿cuántas son?
Y también hemos dado solución al problema planteado la semana pasada (La carrera): La semana pasada Jon y Raúl se retaron a una carrera desde la puerta de EITB hasta el ayuntamiento de Eibar, que está a 46 km. Como Jon vio que Raúl corrÃa menos -de hecho lo hacÃa a una velocidad de 12 km/h- después de haber recorrido 45 km a una velocidad de 15 km/h, se paró a charlar con unos amigos durante una hora -seguro de su victoria- y luego siguió. ¿Quién ganó la carrera, Jon o Raúl?
La solución es: Ganó Raúl. Jon tardó 3 horas en recorrer 45 km, y además estuvo otra hora de charla, mientras que Raúl en esas 4 horas recorrió 4 x 12 = 48 km.)
El libro recomendado hoy es: Mapas del metro y redes neuronales. La teorÃa de grafos, Claudi Alsina, RBA, 2010 (dentro de la colección âEl mundo es matemáticoâ).
