En nuestra sección biisemanal de matemáticas con Raul Ibáñez hablamos sobre una conocida sucesión de números, conocida como la sucesión de Fibonacci, que es otro de esos temas matemáticos que ha trascendido la ciencia para adentrase en la cultura. Podéis escuchar aquí la charla que hemos mantenido hoy.

Para empezar, recordemos cual es la sucesión de Fibonacci y su origen. Esta sucesión infinita de números aparece asociada al famoso problema de los conejos que Leonardo de Pisa (1170-1241), conocido como Fibonacci, plantea (entre otros problemas) en su libro “Liber Abaci” (1202, El libro del Ábaco). El problema es el siguiente:

“Consideremos una familia de conejos con la característica de que tardan un mes en ser fértiles. Cuando han alcanzado la fertilidad, cada pareja se aparea teniendo al mes siguiente (cada hembra) una pareja de crías (un macho y una hembra) que de nuevo tardarán en ser fértiles un mes y entonces se aparearán. Así, según va transcurriendo el tiempo, irá aumentando el número de parejas de conejos. Fibonacci preguntó cuántas parejas de conejos habría al cabo de un tiempo dado.”

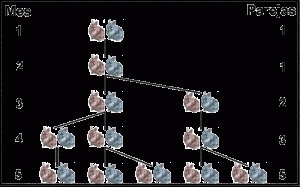
Lo mejor para ver la evolución de parejas de conejos, mes a mes, es hacer un árbol genealógico (mes a mes) desde la pareja inicial, es decir, un esquema en el que ir poniendo las parejas que hay cada mes y las crías que tienen.

No es difícil darse cuenta de que la sucesión del número de parejas de conejos que hay cada mes

1   1   2   3   5   8   13   21   34   55   89   144   233   377   610  …

Tiene la propiedad de que cada término de la sucesión es la suma de los dos términos anteriores. La razón es sencilla, y se ve claramente si miramos el esquema por meses, ya que cada mes estarán las parejas del mes anterior más las nuevas parejas que serán las crías de las parejas fértiles en ese momento, es decir, las que estaban dos meses antes.

Aunque pueda sorprender, los números de Fibonacci están muy presentes en botánica, y más concretamente en la filotaxis, una parte de la morfología vegetal que se dedica al estudio de la composición, ordenación y disposición de las hojas (filos) a lo largo de los tallos, así como de los brotes o las semillas. Por ejemplo, en las espirales de los girasoles y piñas, o en la disposición helicoidal de las hojas en el tallo, aparecen los números de Fibonacci.

Para que nuestras oyentes, y nuestros oyentes, se hagan una idea, vamos aponer un ejemplo. El número de espirales en algunas “cabezas de semillas” (por ejemplo, los girasoles o las piñas) o en “flores de multitud de pétalos”, no es un número cualquiera sino que “muy frecuentemente” es un número de la sucesión de Fibonacci.

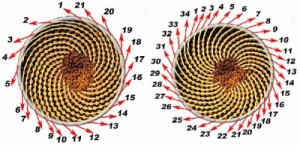
Si cogemos la cabeza de un girasol, vemos que hay dos tipos de espirales, unas en el sentido de las agujas del reloj y otro en el sentido contrario, al contar en número de espirales en ambas direcciones nos dan dos números consecutivos de la sucesión de Fibonacci (por ejemplo, en la imagen que tenemos aquí de un girasol, hay 21 espirales en un sentido y 34 en el otro, es decir, dos números consecutivos de la sucesión de Fibonacci). No siempre son estos dos, en otros ejemplos he visto 34 y 55, o 55 y 89. O en la piña de piñones o las frutas que tenemos en nuestra nevera. De hecho, si nos fijamos bien, realmente existen tres clases distintas de espirales, que al contarlas nos salen tres números consecutivos de la sucesión. Por ejemplo, 5, 8 y 13.

Al parecer, la razón para esta distribución está en la forma de buscar un empaquetamiento óptimo de las semillas, compatible con el crecimiento de la cabeza de semillas. Las semillas tienen que ir distribuyéndose alrededor del centro de forma que no dejen espacios libres y que ocupen el menor espacio posible. Para ello se van distribuyendo alrededor del centro con un cierto ángulo respecto a la semilla anterior, ese ángulo está relacionado con el número de oro (el cual está relacionado con la sucesión de Fibonacci, pero ese es otro tema).

Esta sucesión ha llamado la atención de muchas personas, y ha sido utilizado en diferentes manifestaciones culturales. Veamos algunos ejemplos.

Literatura. La sucesión de Fibonacci aparece, por ejemplo, en el bestseller mundial “El código da Vinci” (Umbriel, 2004) de Dan Brown. Aparece en varias ocasiones a lo largo de la novela. Al principio de la novela, en la escena del crimen del conservador del Museo del Louvre, Jacques Saunière, aparecen pintados en el suelo de la galería los números 13-3-2-21-1-1-8-5. Ni la policía, ni el protagonista (Langdon) saben cuál es el significado de esa serie de números. Pero nosotros si lo sabemos, son los ocho primeros números de Fibonacci, pero desordenados.

Posteriormente estos dígitos ordenados se convertirán en el número de cuenta que da acceso a una caja de depósitos de un banco. Además, en cierto momento, se explica que la sucesión de Fibonacci está relacionada con el número de oro, la divina proporción, así como su relación con el arte y la naturaleza.

Poesía. Algunos poetas han hecho uso de la sucesión de Fibonacci para definir la estructura de sus poemas. Así, la escritora danesa Inger Christensen (1935-2009) la utiliza en una de sus obras más conocida “Alfabet” (Alfabeto), de 1981. Esta poetisa trabaja con dos restricciones en su poema, el alfabeto, de la A hasta la N, y la sucesión de Fibonacci (1 2 3 5 8 13 21 34…610). Cada una de las estrofas de “Alfabet” se inicia con la correspondiente letra del alfabeto, desde la A de Albaricoque a la N de Noche, y de hecho esa letra está presente en toda la estrofa (véase en el trozo del poema que se muestra más abajo). Pero además, el número de versos de cada estrofa se corresponde con cada uno de los números de Fibonacci, así la primera estrofa, correspondiente a la letra A, tiene 1 verso, la segunda, relacionada con la letra B, tiene 2 versos, la estrofa de la letra C tiene 3 versos, 5 versos la de la letra D, y así hasta completar las 14 estrofas del poema.

Arte. En un par de ocasiones hemos podido ver en el Museo Guggenheim de Bilbao la obra “Crocodrilus Fibonacci” (1972) del artista italiano Mario Merz (1925-2003). Esta instalación consiste en un cocodrilo seguido por una sucesión de números en neón, exactamente los números de Fibonacci. Es muy probable que Merz esté jugando aquí con la misma idea de los conejos, pero trasladada a los cocodrilos.

El artista Mario Merz, perteneciente al movimiento Arte Povera (arte pobre en italiano) se ha hecho famoso por sus numerosas y variadas instalaciones con los números de fibonacci en neón. Le fascinaba la geometría de la naturaleza, y especialmente la sucesión de Fibonacci y las espirales, que también aparecen en varias de sus obras. Un ejemplo es una chimenea en Turku (Finlandia) en un proyecto artístico relacionado con el medio ambiente (1994), en la que encontramos la sucesión de Fibonacci a lo largo de la chimenea, desde el número 1 hasta el número 55.

Otro ejemplo es “Sin Título (A real sum is a sum of people)” (1972), en el que vemos fotografías de una escena y entre foto y foto hay un número de fibonacci. Las fotografías tienen el mismo escenario, un café o restaurante, pero en cada foto hay tantas personas como indica el número de fibonacci en neón que acompaña la fotografía.

También incluye los números de Fibonacci en varios de sus famosos igloos, como “La casa de Pitágoras” (1994) o “Lugares sin calles” (1987). Y así podríamos hablar de una gran cantidad de instalaciones realizadas por Merz que hacen uso de estos números, como “Crescendo appare” (1992), que está en  el Paseo Joan de Borbó de Barcelona.

 

Pero no es el único artista, ni mucho menos, que utiliza la sucesión de Fibonacci. Como por ejemplo la famosa serie de esculturas “Ratio” (proporción) realizadas por el escultor australiano de Land Art, Andrew Rogers (Israel, India, Sri Lanka,…). Está formada por bloques, con forma de prisma de cara cuadrada, dispuestos en columnas distribuidas de simétricamente de alturas iguales a un capicúa de Fibonacci, 1 1 2 3 5 8 5 3 2 1 1 (o llegando también a 13). Pero en esta obra como en otras muchas no aparecen los números explícitamente (es la cantidad de bloques de cada columna de la escultura).

 

Música. Es bastante conocido que el compositor húngaro Béla Bartók (1881-1945) utilizó esta sucesión de números para desarrollar una escala musical que denominó “escala fibonacci”. Quien esté interesado en este tema puede leer el artículo de Iñigo Ibaibarriaga “Música y Matemáticas, de Schoenberg a Xenakis”  (que se puede encontrar en divulgamat). Ibaibarriaga también comenta que quizás uno de los primeros usos de la sucesión de Fibonacci en la música podría ser la quinta sinfonía de Beethoven, aunque podría no ser una utilización intencionada.

Cine. En la película de Aronofsky, “Pi, Fé en el caos” el protagonista describe la sucesión de Fibonacci y la espiral que se construye a partir de ella, como hemos visto.

Retos matemáticos

Problema (un problema clásico de monedas): ¿De qué forma podemos colocar 10 monedas dentro de 3 vasos de forma que haya un número impar de monedas en cada uno de ellos?

Solución Problema (factorial): Empecemos recordando que significa en matemáticas la operación factorial, es la multiplicación de todos los números desde uno hasta el que nos interesa, así, 4! = 4 x 3 x 2 x 1 = 24. Resulta que le he pedido a mi ordenador que calcule el factorial de 20, 20!, pero al imprimirlo han salido borrosos las cinco últimas cifras, así

20! = 2.432.902.008.176.6AB.CDE

El problema consiste en adivinar el valor de esas últimas cinco cifras (A, B, C, D y E), sin hacer la cuenta.Solución: Teniendo en cuenta que al realizar el factorial de 20, se multiplican los números 20, 10, 15, 5, 4, 2 tenemos cuatro multiplicaciones del número 10, luego los cuatro últimos números –correspondientes a B, C, D, E- son ceros. Ahora, ¿cómo averiguar qué número es A? De nuevo por una cuestión de divisibilidad… al realizar el factorial de 20, en particular, se multiplica por 9, luego el número resultante es múltiplo de 9, luego si sumamos todas sus cifras también lo será… luego sumamos todas menos A y nos da 50, luego el siguiente múltiplo de 9 es el 54, es decir, A=4

* LIBRO RECOMENDADO: Teresa Navarro, Buscando a LO, puntodepapel, 2014.