Si escribes los números que van del 1 al 100 inclusive, ¿Cuántos unos habrás escrito?

Solución: 21 unos. Los unos (1) de los números que terminan con la cifra 1, que son 10, los unos (1) de los números que empiezan por esa cifra, que son 10 de dos cifras y una de tres, en total, 21Solución: 21 unos. Los unos (1) de los números que terminan con la cifra 1, que son 10, los unos (1) de los números que empiezan por esa cifra, que son 10 de dos cifras y una de tres, en total, 21

Dos trenes que van por la misma vía y en dirección contraria, han partido de dos estaciones alejadas entre sí 1.800 km. Los trenes circulan a la velocidad de 170 km/h uno y 190 km/h el otro. ¿A qué distancia estarán uno del otro un minuto antes de estrellarse?

Solución: 6 kilómetros. La velocidad relativa de los dos trenes es de 170 + 190 = 360 Km/h, es decir, de 6 km por minuto, luego esa es la distancia entre los trenes un minuto antes de estrellarse, 6 km

Tengo 48 caramelos en tres bolsas. Si de la primera bolsa paso a la segunda tantos caramelos como hay en la tercera, después paso de la segunda bolsa 6 caramelos a la primera y, para finalizar, paso a la tercera bolsa 4 caramelos de la segunda. El resultado es que ahora tengo la misma cantidad de caramelos en las tres bolsas. ¿Cuántos caramelos tenía inicialmente en cada una de las bolsas?

Solución: Los caramelos de cada bolsa son 22, 14 y 12. Se resuelve con un poco de álgebra. Si llamamos x, y , z a la cantidad de caramelos que hay en cada bolsa, las condiciones del problema nos dicen que [x + y + z = 48] y que [x – z + 6 = y + z – 10 = z + 4], luego resolviendo el sistema se obtiene que x = 22, y = 14 y z = 12.)

Maite y Aitor revisan lo que tienen en sus bolsillos con el fin de saber si podrán comprar un juguete de moda. A Maite le faltan 19 euros para comprar el juguete, mientras que a Aitor le faltan 2 euros. Ni siquiera juntando el dinero de ambos les alcanza para comprar el juguete. ¿Cuánto cuesta el juguete de moda?

Solución: El juguete cuesta 20 euros. Aitor tendrá 18 euros y Maite 1 euro, suponiendo que los dos tienen dinero y una cantidad entera de euros.

Si llamamos A a la cantidad de euros que tiene Aitor y M a la que tiene Maite, se tiene que la cantidad que cuesta el juguete es M + 19 = A + 2, ya que Maite le faltan 19 euros para comprar el juguete, mientras que a Aitor le faltan 2 euros. Como juntos no pueden comprar el juguete, se tiene que M + A es más pequeño que M + 19 = A + 2, luego A es más pequeño que 19 –Aitor tiene menos de 19 euros- y M es más pequeño que 2 –Maite tiene menos de dos euros-. Pero si Maite tiene dinero tendrá, entonces, 1 euro, luego Aitor tendrá 18 euros, ya que M + 19 = A + 2)

Un hombre tenía en su oficina tres armarios, cada uno de los cuales contenía nueve casilleros, como se muestra en el diagrama. Le dijo a su empleado que colocara un número de una cifra diferente en cada taquilla del armario A, y que hiciera lo mismo en el caso de B, y de C.

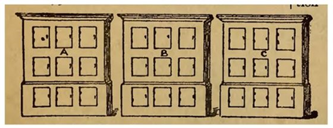
Ahora bien, el empresario no dijo que los armarios debían ser numerados en ningún orden numérico, y se sorprendió al encontrar, cuando el trabajo estaba hecho, que las cifras habían sido aparentemente mezcladas indiscriminadamente. Al pedirle explicaciones a su empleado, el excéntrico muchacho le dijo que se le había ocurrido ordenar las cifras de manera que en cada caso formaran una simple suma, las dos filas superiores de cifras producían la suma de la fila inferior. Pero el punto más sorprendente era éste: que los había dispuesto de tal manera que la suma en A daba la menor suma posible, que la suma en C daba la mayor suma posible, y que los nueve dígitos de los tres resultados totales de las sumas eran diferentes. El acertijo consiste en mostrar cómo se puede hacer esto. No se admiten decimales y el cero no puede aparecer en el lugar de la centena.

(Nota: El problema está pidiendo que se busquen tres sumas pandigitales (con cero incluido) del tipo ABC + DEF = GHI, la primera la más pequeña posible y la tercera la más grande posible, junto con una última condición, que los resultados de las tres sumas sea pandigital también)

Solución: Como decíamos, nos está pidiendo que busquemos tres sumas del tipo ABC + DEF = GHI. La suma más pequeña de este tipo es 107 + 249 = 356 (que iría en el primer armario), mientras que la suma más grande es 235 + 746 = 981, o también, 324 + 657 = 981 (una de ellas iría en el tercer armario). Como los resultados de esas dos sumas son 356 y 981, entonces el resultado de la suma del armario del centro debe de tener tres de las cifras restantes, es decir, 0, 2, 4, 7. Por lo tanto, las sumas posibles para el armario del centro son 134 + 586 = 720, 134 + 568 = 702 ó 138 + 269 = 407.

En una frutería hay seis cajas de manzanas, salvo una que es de peras. El primer cliente que llega se lleva una cierta cantidad de manzanas, mientas que el siguiente cliente se lleva el doble de manzanas que el anterior y el frutero se queda sin manzanas. Sabiendo que en la frutería solamente se venden cajas completas de fruta y que cada caja lleva marcado el número de manzanas que contiene (a saber, 15, 16, 18, 19, 20 y 31), ¿cuál es la caja de peras?

Solución: Los clientes compraron las siguientes cajas de manzanas: el primero las cajas de 15 y 18 manzanas, mientras que el segundo las cajas con 16, 19 y 31 manzanas, luego la caja de peras es la que tenía 20 unidades

Como todos sabemos las sandías tienen una gran cantidad de agua. Cuando están frescas el 99% es agua. En cierta ocasión un agricultor había sacado de su huerta 100 kilos de sandías frescas, pero al estar varios días al sol esperando que viniera un camión a recogerlas estas se secaron un poco, y pasaron a tener un contenido del 98% en agua. ¿Cuánto pesaban las sandías cuando las recogió el camión?

Solución: Las sandías pesan 50 kilos. De los 100 kilos que pesan las sandías, el 1% no es agua, es decir, 1 kilo. Por otra parte, al secarse las sandías el contenido en agua a pasado a ser del 98%, luego la parte sólida es ahora del 2%, que es 1 kilo, como hemos comentado. Pero 1 kilo es el 2% de 50 kilos, que será lo que pesan las sandías cuando las recogió el camión

Disponemos de las 7.890 piedras del problema anterior y queremos separarlas en tres montones de forma que, si dividimos la cantidad de piedras del primer montón por 3, la del segundo por 6 y la de tercero por 9, el cociente es, en los tres casos, el mismo número.

Solución: Los tres montones constan de 1.315, 2.630 y 3.945 piedras. La solución se obtiene de la siguiente forma. Si consideramos que la cantidad de piedras de cada montón es x, y, z, entonces la suma es 7.890, esto es, x + y + z = 7.890. Además, las condiciones del problema nos dicen x / 3 = y / 6 = z / 9, de donde z = 3 x, y = 2x. Introduciendo esto en la ecuación primera tenemos que x = 1.315, y = 2.630 y z = 3.945

Estas navidades le he regalado a uno de mis amigos un rompecabezas matemático y un libro. Cinco veces el precio del rompecabezas era exactamente igual a doce veces el precio del libro, y los dos juntos costaron 85 euros.  ¿Cuál fue el precio de cada uno?

Solución: El rompecabezas matemático costó 60 euros y el libro 25 euros. Este problema se resuelve fácilmente con ecuaciones algebraicas. Si el precio del juego es x euros y el del libro y euros, entonces las condiciones del problema nos dicen que 5 x = 12 y, así como que x + y = 85. Resolviendo el sistema de ecuaciones se obtiene que x = 60 e y = 25

¿Cuál es el número de dos dígitos tal que su valor es igual a cinco veces la suma de sus dígitos y si se suma nueve al número se obtiene un número con los mismos dígitos que el número original, pero con el orden cambiado?

Solución: El número es 45. Para resolverlo se considera que el
número de los dígitos es “ab”, luego su valor es 10a + b. Por las
condiciones del problema tenemos que 10a + b = 5 x (a + b) y
10a + b + 9 = 10 b + a. Despejando en la segunda ecuación se
tiene que b = a + 1. Y pasando esto a la primera, a = 4, de donde b
=5