Una caja de cereales (de medidas 12 cm. x 25 cm. x 36 cm.) está tirada en el suelo de la cocina (apoyada en una de las caras de dimensiones 25 x 36). Una hormiga está en el suelo, justo en una de las esquinas de la caja y tiene que ir a la esquina opuesta en el suelo ¿Cuál es la longitud del camino más corto que puede realizar?

Solución: La solución es raíz cuadrada de (3673) = 60,6. ¿Por qué?

Una posibilidad para la hormiga es ir por el suelo bordeando la caja y así recorrería 25+36=61 cm. Pero ¿es posible realizar un recorrido más corto si subimos por la caja?

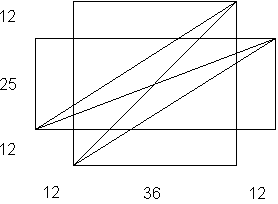
Para dar solución a este problema lo que tenemos que hacer es convertir un problema aparentemente del espacio en un problema del plano, puesto que la hormiga anda por la caja, que salvo en los bordes es plana. Para ello lo que debemos hacer es quitarle la cara de abajo a la caja y cortar los laterales para poder desplegarla en el suelo, obteniendo así la imagen siguiente

En el baserri tenemos gallinas y conejos, de forma que hay 40 cabezas y 110 patas. ¿Cuántas gallinas y conejos hay?

Solución: 15 conejos y 25 gallinas. Por cada pata de gallina hay dos patas de conejo, luego si contamos una pata por gallina y dos por conejo nos da 55 patas (110/2), pero entonces de ellas, como solo hay 40 cabezas, las 15 de diferencia nos computan las segundas patas de los conejos, es decir, hay 15 conejos. Y 40-15=25 gallinas

Un hombre quiere comprar 20 animales por 20 francos, y el precio de los animales es, a saber: bueyes a 5 francos cada uno, cerdos a 2 francos cada uno y corderos a ½ franco cada uno. Se pregunta, ¿Cuántos bueyes, cerdos y corderos habrá en la compra?

Solución:   Si llamamos x al número de bueyes que compra, y cerdos, z corderos. Teniendo en cuenta el enunciado del problema obtenemos las siguientes ecuaciones: x+y+z=20; 5x+2y+z/2=20. Sin embargo, si intentamos solucionarlo obtenemos una contradicción, por ejemplo, simplificando la z obtenemos que 9x+3y=20, lo que implicaría que 20 es divisible por 3, imposible

¿Qué hora es, si quedan del día la tercera parte de las horas que han pasado?

Solución: Si queda la tercera parte de las horas que han pasado del día, lo que quedan es un cuarto de todas las horas del día. Como el día tiene 24 horas, faltan aún 6 horas para que termine el día, luego son las 18:00 horas

La semana pasada regalé libros en cuatro centros escolares. En cada centro dejé la mitad de los libros que llevaba más medio libro, y después del cuarto centro escolar no me quedaba ningún libro más a repartir, ¿Cuántos libros llevaba inicialmente? ¿Cuántos repartí en cada centro? (nota: a mí me gustan los libros, por lo que yo no corto libros por la mitad.)

Solución: 15.

Podemos resolver este problema planteando una ecuación matemática o simplemente actuando con lógica desde atrás hacia delante. Como acabamos con 0 libros, al llegar al último centro teníamos 1 libro, la mitad más medio es igual a 1, y no nos sobra ningún libro. Y poco a poco vamos viendo que el número de libros al llegar a cada centro es 1, 3, 7, 15

Un aizkolari tarda 20 minutos en partir un tronco de 6 metros en tres partes iguales. ¿Cuánto tiempo tardará en partir en seis partes iguales un tronco igual de grueso que mida 12 metros?

Solución: 50 minutos. Para cortar un tronco de 6 metros en tres partes, el aizkolari debe de cortar por dos lugares distintos, y para partir un tronco de 12 metros en 6 partes iguales, deberá cortar por 5 lugares distintos. Si en dos cortes tarda 20 minutos, en cinco tardará 50 minutos

Imaginemos que tenemos todas las fichas del juego de las damas, que son 24 fichas, desparramadas sobre la mesa y que queremos hacer una pila única con todas ellas. ¿Cómo hacerlo para realizar el número mínimo de movimientos? ¿Apilándolas de una en una o haciendo primero pequeños montones y luego apilar estos?

(nota: mover una ficha o un montón se considera un único movimiento)

Solución: Da lo mismo, el número de movidas es el mismo, no importa cómo lo hagamos